URL: https://zm1.desy.de/e34/e727/index_ger.html
Breadcrumb Navigation
FEM Berechnungen
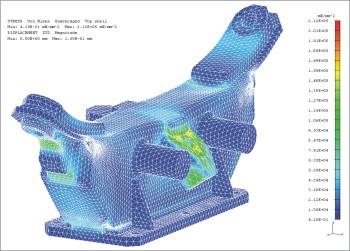
Die Finite-Elemente-Methode (oder kurz FEM) ist ein numerisches Verfahren zur näherungsweisen Lösung, insbesondere elliptischer partieller Differentialgleichungen mit Randbedingungen. Sie ist auch ein weit verbreitetes modernes Berechnungsverfahren im Ingenieurwesen.1
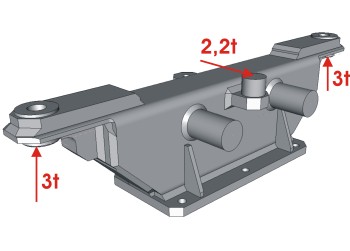
Ziel der FEM ist die Bestimmung der Verformungen und Spannungen, die durch zum Beispiel äußere Kräfte, Verformungen und Temperaturschwankungen innerhalb eines Bauteiles hervorgerufen werden.
Für die Berechnung wird das Berechnungsgebiet in eine große Zahl endlich vieler definierter Elemente zerlegt und vernetzt. Daher der Name Finite-Elemente-Methode. Auf diesen Elementen werden nun Ansatzfunktionen definiert, aus denen sich über die partielle Differentialgleichung und die Randbedingungen ein Gleichungssystem ergibt. Aus dem gelösten Gleichungssystem werden die gesuchten Größen abgeleitet.
Die Methode ist ein Näherungsverfahren. Die Genauigkeit hängt von der Anzahl der Elemente pro Flächeneinheit ab. Um die Realität exakt abzubilden wären unendlich viele (infinite) Elemente nötig. Deshalb ist bei der FEM immer ein Kompromiss zwischen der geforderten Genauigkeit und der zur Verfügung stehenden Rechenkapazität zu finden.
ZM1 nutzt ANSYS für die Berechnung von Bauteilen. Anwendung finden auch die vereinfachten Möglichkeiten der FEM, welche in SolidEdge und I-DEAS "eingebettet" sind.
Für die sichere Bewertung der Ergebnisse sollte der Anwender erfahren im Umgang mit der FEM sein, die Konstrukteure von ZM1 stehen Ihnen natürlich gern hilfreich zur Seite.
Bei Interesse an einer FEM-Auftragsberechnung wenden Sie sich bitte an den Fachgruppenleiter Herrn Martens.
1:http://de.wikipedia.org/wiki/Finite-Elemente-Methode
FEM- Referenz
Quelle der Abbildungen: Homepage von Thorsten Stoye
